Sapling extended keys

BIP 32 defines a method to derive a number of child keys from a parent key. In order to prevent these from depending solely on the parent key itself, both the private and public keys are extended with a 32-byte chain code. We similarly extend Sapling keys with a chain code here. However, the concepts of "private" and "public" keys in BIP 32 do not map cleanly to Sapling's key components. We take the following approach:

• We derive child Sapling expanded spending keys, rather than Sapling spending keys. This enables us to implement both hardened and non-hardened derivation modes (the latter being incompatible with Sapling spending keys).
• We do not derive Sapling public keys directly, as this would prevent the use of diversified addresses. Instead, we derive Sapling full viewing keys, from which payment addresses can be generated. This maintains the trust semantics of BIP 32: someone with access to a BIP 32 extended public key is able to view all transactions involving that address, which a Sapling full viewing key also enables.

We represent a Sapling extended spending key as \((\mathsf{ask, nsk, ovk, dk, c})\!\) , where \((\mathsf{ask, nsk, ovk})\) is the normal Sapling expanded spending key, \(\mathsf{dk}\) is a diversifier key, and \(\mathsf{c}\) is the chain code.

We represent a Sapling extended full viewing key as \((\mathsf{ak, nk, ovk, dk, c})\!\) , where \((\mathsf{ak, nk, ovk})\) is the normal Sapling full viewing key, \(\mathsf{dk}\) is the same diversifier key as above, and \(\mathsf{c}\) is the chain code.

Sapling helper functions

Define

• \(\mathsf{EncodeExtSKParts}(\mathsf{ask, nsk, ovk, dk}) :=\) \(\mathsf{I2LEOSP}_{256}(\mathsf{ask})\) \(||\,\mathsf{I2LEOSP}_{256}(\mathsf{nsk})\) \(||\,\mathsf{ovk}\) \(||\,\mathsf{dk}\)
• \(\mathsf{EncodeExtFVKParts}(\mathsf{ak, nk, ovk, dk}) :=\) \(\mathsf{LEBS2OSP}_{256}(\mathsf{repr}_\mathbb{J}(\mathsf{ak}))\) \(||\,\mathsf{LEBS2OSP}_{256}(\mathsf{repr}_\mathbb{J}(\mathsf{nk}))\) \(||\,\mathsf{ovk}\) \(||\,\mathsf{dk}\)

Sapling master key generation

Let \(S\) be a seed byte sequence of a chosen length, which MUST be at least 32 and at most 252 bytes.

• Calculate \(I = \mathsf{BLAKE2b}\text{-}\mathsf{512}(\texttt{“ZcashIP32Sapling”}, S)\!\) .
• Split \(I\) into two 32-byte sequences, \(I_L\) and \(I_R\!\) .
• Use \(I_L\) as the master spending key \(\mathsf{sk}_m\!\) , and \(I_R\) as the master chain code \(\mathsf{c}_m\!\) .
• Calculate \(\mathsf{ask}_m\!\) , \(\mathsf{nsk}_m\!\) , and \(\mathsf{ovk}_m\) via the standard Sapling derivation 11:
  • \(\mathsf{ask}_m = \mathsf{ToScalar^{Sapling}}(\mathsf{PRF^{expand}}(\mathsf{sk}_m, [\mathtt{0x00}]))\)
  • \(\mathsf{nsk}_m = \mathsf{ToScalar^{Sapling}}(\mathsf{PRF^{expand}}(\mathsf{sk}_m, [\mathtt{0x01}]))\)
  • \(\mathsf{ovk}_m = \mathsf{truncate}_{32}(\mathsf{PRF^{expand}}(\mathsf{sk}_m, [\mathtt{0x02}]))\!\) .
• Calculate \(\mathsf{dk}_m\) similarly:
  • \(\mathsf{dk}_m = \mathsf{truncate}_{32}(\mathsf{PRF^{expand}}(\mathsf{sk}_m, [\mathtt{0x10}]))\!\) .
• Return \((\mathsf{ask}_m, \mathsf{nsk}_m, \mathsf{ovk}_m, \mathsf{dk}_m, \mathsf{c}_m)\) as the master extended spending key \(m_\mathsf{Sapling}\!\) .

Note that the master extended key is invalid if \(\mathsf{ask}_m\) is \(0\!\) , or if the corresponding \(\mathsf{ivk}\) derived as specified in 11 is \(0\!\) .

Sapling child key derivation

As in BIP 32, the method for deriving a child extended key, given a parent extended key and an index \(i\!\) , depends on the type of key being derived, and whether this is a hardened or non-hardened derivation.

Sapling internal key derivation

The above derivation mechanisms produce external addresses suitable for giving out to senders. We also want to be able to produce another address derived from a given external address, for use by wallets for internal operations such as change and auto-shielding. Unlike BIP 44 that allows deriving a stream of external and internal addresses in the same hierarchical derivation tree 5, for any external full viewing key we only need to be able to derive a single internal full viewing key that has viewing authority for just internal transfers. We also need to be able to derive the corresponding internal spending key if we have the external spending key.

Deriving a Sapling internal full viewing key

Let \(\mathcal{H}^\mathsf{Sapling}\) be as defined in 11.

Let \((\mathsf{ak}, \mathsf{nk}, \mathsf{ovk}, \mathsf{dk})\) be the external full viewing key.

• Let \(I = \textsf{BLAKE2b-256}(\texttt{“Zcash\_SaplingInt”}, \mathsf{EncodeExtFVKParts}(\mathsf{ak}, \mathsf{nk}, \mathsf{ovk}, \mathsf{dk}))\!\) .
• Let \(I_\mathsf{nsk} = \mathsf{ToScalar^{Sapling}}(\mathsf{PRF^{expand}}(I, [\mathtt{0x17}]))\!\) .
• Let \(R = \mathsf{PRF^{expand}}(I, [\mathtt{0x18}])\!\) .
• Let \(\mathsf{nk_{internal}} = [I_\mathsf{nsk}] \mathcal{H}^\mathsf{Sapling} + \mathsf{nk}\!\) .
• Split \(R\) into two 32-byte sequences, \(\mathsf{dk_{internal}}\) and \(\mathsf{ovk_{internal}}\!\) .
• Return the internal full viewing key as \((\mathsf{ak}, \mathsf{nk_{internal}}, \mathsf{ovk_{internal}}, \mathsf{dk_{internal}})\!\) .

This design uses the same technique as non-hardened derivation to obtain a full viewing key with the same spend authority (the private key corresponding to \(\mathsf{ak}\!\) ) as the original, but viewing authority only for internal transfers.

The values of \(I\!\) , \(I_\mathsf{nsk}\!\) , and \(R\) are the same between deriving a full viewing key, and deriving the corresponding spending key. Both of these derivations are shown in the following diagram:

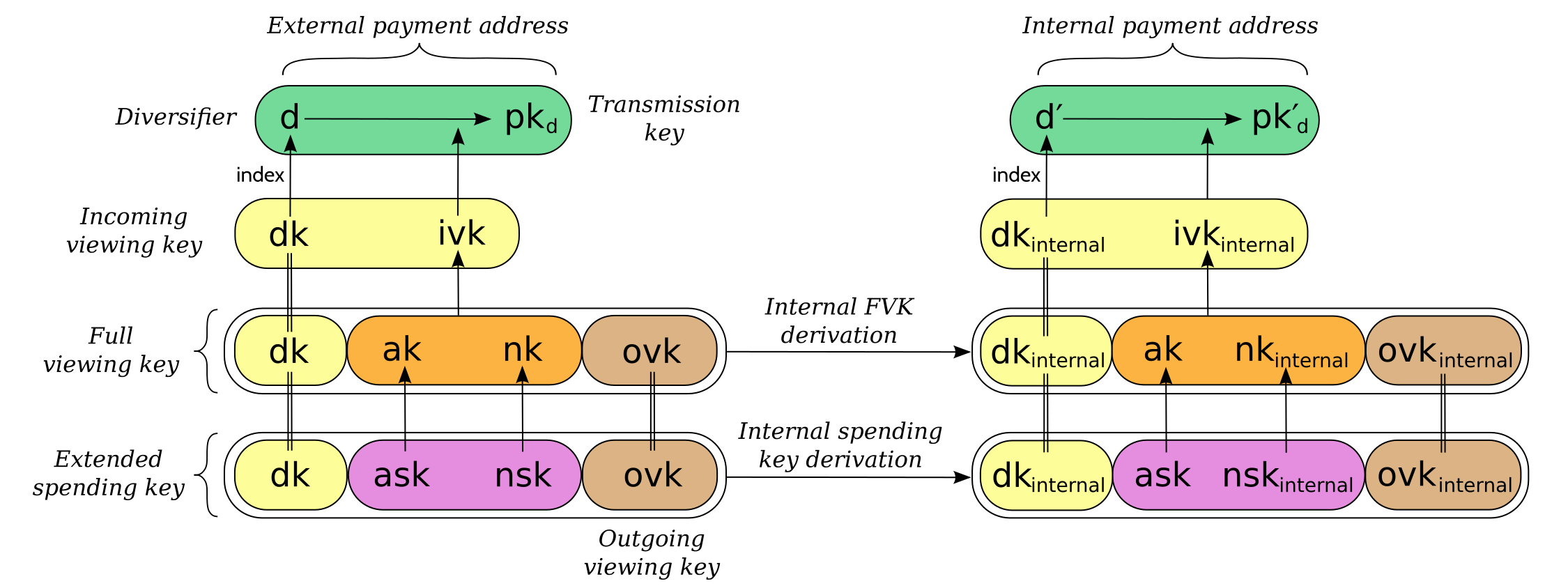
(For simplicity, the proof authorizing key is not shown.)

This method of deriving internal keys is applied to external keys that are children of the Account level. It was implemented in zcashd as part of support for ZIP 316 8.

Note that the internal extended key is invalid if \(\mathsf{ak}\) is the zero point of Jubjub, or if the corresponding \(\mathsf{ivk_{internal}}\) derived from the internal full viewing key as specified in 11 is \(0\!\) .

Sapling diversifier derivation

The 88-bit diversifiers for a Sapling extended key are derived from its diversifier key \(\mathsf{dk}\!\) . To prevent the diversifier leaking how many diversified addresses have already been generated for an account, we make the sequence of diversifiers pseudorandom and uncorrelated to that of any other account. In order to reach the maximum possible diversifier range without running into repetitions due to the birthday bound, we use FF1-AES256 as a Pseudo-Random Permutation as follows:

• Let \(j\) be the index of the desired diversifier, in the range \(0\,..\, 2^{88} - 1\!\) .
• \(d_j = \mathsf{FF1}\text{-}\mathsf{AES256.Encrypt}(\mathsf{dk}, \texttt{“”}, \mathsf{I2LEBSP}_{88}(j))\!\) .

A valid diversifier \(d_j\) is one for which \(\mathsf{DiversifyHash^{Sapling}}(d_j) \neq \bot\!\) . For a given \(\mathsf{dk}\!\) , approximately half of the possible values of \(j\) yield valid diversifiers.

The default diversifier for a Sapling extended key is defined to be \(d_j\!\) , where \(j\) is the least nonnegative integer yielding a valid diversifier.

Instantiation

Let \(\mathsf{Context}\) be the context in which the hardened-only key derivation process is instantiated (e.g. a shielded protocol). We define two context-specific constants:

• \(\mathsf{Context.MKGDomain}\) is a sequence of 16 bytes, used as a domain separator during master key generation. It SHOULD be disjoint from other domain separators used with BLAKE2b in Zcash protocols.
• \(\mathsf{Context.CKDDomain}\) is a byte value, used as a domain separator during child key derivation. This should be tracked as part of the global set of domains defined for \(\mathsf{PRF^{expand}}\!\) .

Hardened-only master key generation

Let \(\mathsf{IKM}\) be an input key material byte sequence, which MUST use an unambiguous encoding within the given context, and SHOULD contain at least 256 bits of entropy. It is RECOMMENDED to use a prefix-free encoding, which may require the use of length fields if multiple fields need to be encoded.

\(\mathsf{MKGh}^\mathsf{Context}(\mathsf{IKM}) \rightarrow (\mathsf{sk}_m, \mathsf{c}_m)\) :

• Calculate \(I = \mathsf{BLAKE2b}\text{-}\mathsf{512}(\mathsf{Context.MKGDomain}, \mathsf{IKM})\!\) .
• Split \(I\) into two 32-byte sequences, \(I_L\) and \(I_R\!\) .
• Use \(I_L\) as the master secret key \(\mathsf{sk}_m\!\) .
• Use \(I_R\) as the master chain code \(\mathsf{c}_m\!\) .
• Return \((\mathsf{sk}_m, \mathsf{c}_m)\!\) .

Hardened-only child key derivation

\(\mathsf{CKDh}^\mathsf{Context}((\mathsf{sk}_{par}, \mathsf{c}_{par}), i)\) \(\rightarrow (\mathsf{sk}_i, \mathsf{c}_i)\) :

• Check whether \(i \geq 2^{31}\) (whether the child is a hardened key).
  • If so (hardened child): let \(I = \mathsf{PRF^{expand}}(\mathsf{c}_{par}, [\mathsf{Context.CKDDomain}]\,||\,\mathsf{sk}_{par}\,||\,\mathsf{I2LEOSP}_{32}(i))\!\) .
  • If not (normal child): return failure.
• Split \(I\) into two 32-byte sequences, \(I_L\) and \(I_R\!\) .
• Use \(I_L\) as the child secret key \(\mathsf{sk}_i\!\) .
• Use \(I_R\) as the child chain code \(\mathsf{c}_i\!\) .
• Return \((\mathsf{sk}_i, \mathsf{c}_i)\!\) .

Orchard extended keys

We represent an Orchard extended spending key as \((\mathsf{sk, c}),\) where \(\mathsf{sk}\) is the normal Orchard spending key (opaque 32 bytes), and \(\mathsf{c}\) is the chain code.

Orchard master key generation

Let \(S\) be a seed byte sequence of a chosen length, which MUST be at least 32 and at most 252 bytes.

• Return \(\mathsf{MKGh}^\mathsf{Orchard}(S)\) as the master extended spending key \(m_\mathsf{Orchard}\!\) .

Orchard child key derivation

\(\mathsf{CKDsk}((\mathsf{sk}_{par}, \mathsf{c}_{par}), i)\) \(\rightarrow (\mathsf{sk}_{i}, \mathsf{c}_i)\) :

• Return \(\mathsf{CKDh}^\mathsf{Orchard}((\mathsf{sk}_{par}, \mathsf{c}_{par}), i)\)

Note that the resulting child spending key may produce an invalid external FVK, as specified in 12, with small probability. The corresponding internal FVK derived as specified in the next section may also be invalid with small probability.

Orchard internal key derivation

As in the case of Sapling, for a given external address, we want to produce another address for use by wallets for internal operations such as change and auto-shielding. That is, for any external full viewing key we need to be able to derive a single internal full viewing key that has viewing authority for just internal transfers. We also need to be able to derive the corresponding internal spending key if we have the external spending key.

Let \(\mathsf{ask}\) be the spend authorizing key if available, and let \((\mathsf{ak}, \mathsf{nk}, \mathsf{rivk})\) be the corresponding external full viewing key, obtained as specified in 12.

Define \(\mathsf{DeriveInternalFVK^{Orchard}}(\mathsf{ak}, \mathsf{nk}, \mathsf{rivk})\) as follows:

• Let \(K = \mathsf{I2LEBSP}_{256}(\mathsf{rivk})\!\) .
• Let \(\mathsf{rivk_{internal}} = \mathsf{ToScalar^{Orchard}}(\mathsf{PRF^{expand}}(K, [\mathtt{0x83}] \,||\, \mathsf{I2LEOSP_{256}}(\mathsf{ak}) \,||\, \mathsf{I2LEOSP_{256}}(\mathsf{nk}))\!\) .
• Return \((\mathsf{ak}, \mathsf{nk}, \mathsf{rivk_{internal}})\!\) .

The result of applying \(\mathsf{DeriveInternalFVK^{Orchard}}\) to the external full viewing key is the internal full viewing key. The corresponding expanded internal spending key is \((\mathsf{ask}, \mathsf{nk}, \mathsf{rivk_{internal}})\!\) .

Unlike Sapling internal key derivation, we do not base this internal key derivation procedure on non-hardened derivation, which is not defined for Orchard. We can obtain the desired separation of viewing authority by modifying only the \(\mathsf{rivk_{internal}}\) field relative to the external full viewing key, which results in different \(\mathsf{dk_{internal}}\!\) , \(\mathsf{ivk_{internal}}\) and \(\mathsf{ovk_{internal}}\) fields being derived, as specified in 12 and shown in the following diagram:

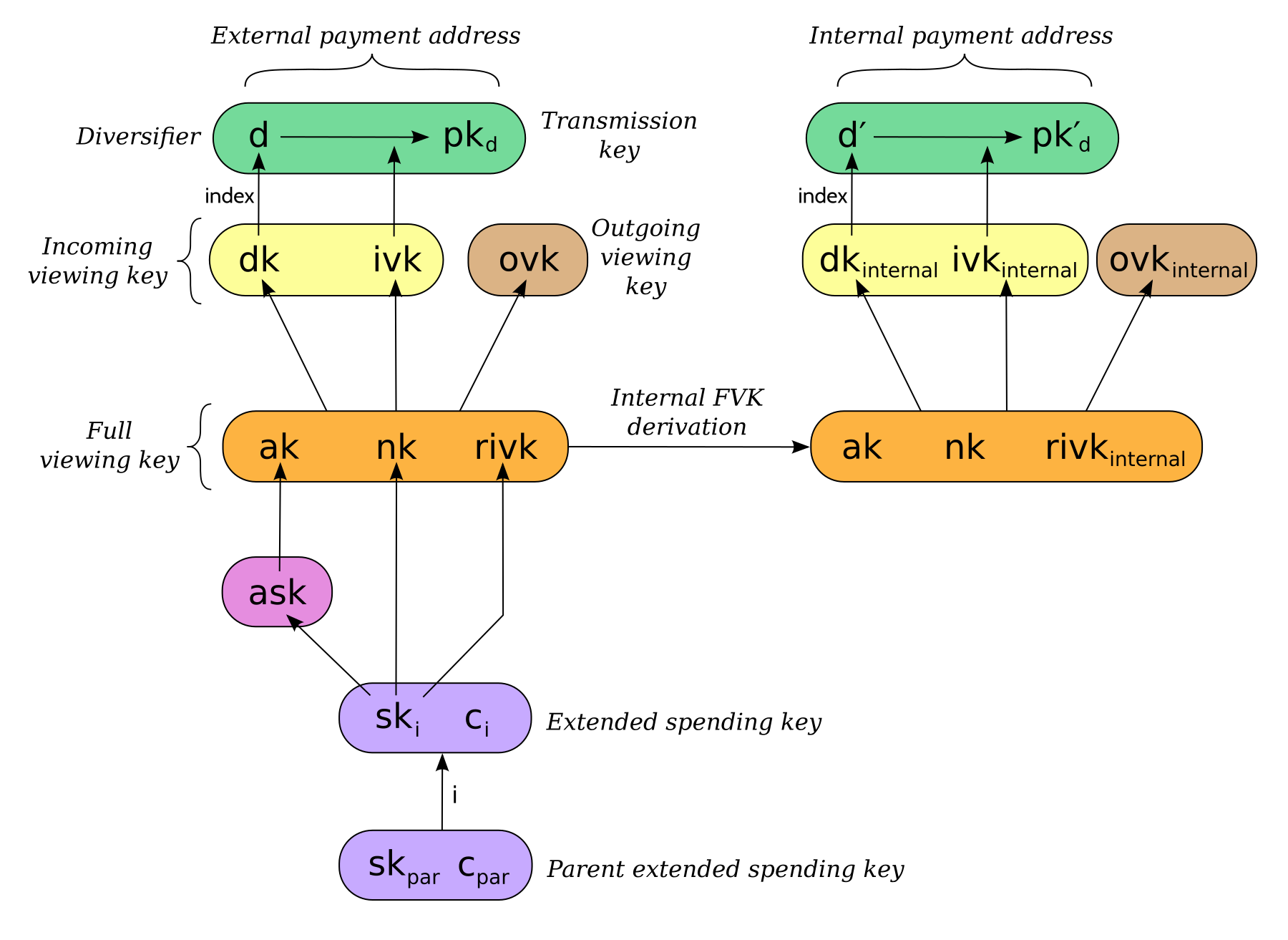
This method of deriving internal keys is applied to external keys that are children of the Account level. It was implemented in zcashd as part of support for ZIP 316 8.

Note that the resulting FVK may be invalid, as specified in 12.

Orchard diversifier derivation

As with Sapling, we define a mechanism for deterministically deriving a sequence of diversifiers, without leaking how many diversified addresses have already been generated for an account. Unlike Sapling, we do so by deriving a diversifier key directly from the full viewing key, instead of as part of the extended spending key. This means that the full viewing key provides the capability to determine the position of a diversifier within the sequence, which matches the capabilities of a Sapling extended full viewing key but simplifies the key structure.

Given an Orchard extended spending key \((\mathsf{sk}_i, \mathsf{c}_i)\!\) :

• Let \((\mathsf{ak}, \mathsf{nk}, \mathsf{rivk})\) be the Orchard full viewing key for \(\mathsf{sk}_i\!\) .
• Let \(K = \mathsf{I2LEBSP}_{256}(\mathsf{rivk})\!\) .
• \(\mathsf{dk}_i = \mathsf{truncate}_{32}(\mathsf{PRF^{expand}}(K, [\mathtt{0x82}] \,||\, \mathsf{I2LEOSP}_{256}(\mathsf{ak}) \,||\, \mathsf{I2LEOSP}_{256}(\mathsf{nk})))\!\) .
• Let \(j\) be the index of the desired diversifier, in the range \(0\,..\, 2^{88} - 1\!\) .
• \(d_{i,j} = \mathsf{FF1}\text{-}\mathsf{AES256.Encrypt}(\mathsf{dk}_i, \texttt{“”}, \mathsf{I2LEBSP}_{88}(j))\!\) .

Note that unlike Sapling, all Orchard diversifiers are valid, and thus all possible values of \(j\) yield valid diversifiers.

The default diversifier for \((\mathsf{sk}_i, \mathsf{c}_i)\) is defined to be \(d_{i,0}.\)

Arbitrary master key generation

Let \(S\) be a seed byte sequence of a chosen length, which MUST be at least 32 and at most 252 bytes.

The master extended arbitrary key is:

\(m_\mathsf{Arbitrary} = \mathsf{MKGh}^\mathsf{Arbitrary}([\mathsf{length}(\mathsf{ContextString})]\,||\,\mathsf{ContextString}\,||\,[\mathsf{length}(S)]\,||\,S)\!\) .

Arbitrary child key derivation

\(\mathsf{CKDarb}((\mathsf{sk}_{par}, \mathsf{c}_{par}), i)\) \(\rightarrow (\mathsf{sk}_i, \mathsf{c}_i)\) :

• Return \(\mathsf{CKDh}^\mathsf{Arbitrary}((\mathsf{sk}_{par}, \mathsf{c}_{par}), i)\!\) .

If the context requires a 64-byte key (for example, to avoid an entropy bottleneck in its particular subsequent operations), and \(i\) is the last element of an HD path, the concatenation \(\mathsf{sk}_i\,||\,\mathsf{c}_i\) MAY be used as a key. In this case, \((\mathsf{sk}_i, \mathsf{c}_i)\) MUST NOT be given as input to \(\mathsf{CKDarb}\) (this is a restatement of the requirement that \(i\) is the last element of an HD path).

Key path levels

Sapling and Orchard key paths have the following three path levels at the top, all of which use hardened derivation:

• \(purpose\!\) : a constant set to \(32'\) (or \(\mathtt{0x80000020}\!\) ) following the BIP 43 recommendation. It indicates that the subtree of this node is used according to this specification.
• \(coin\_type\!\) : a constant identifying the cryptocurrency that this subtree's keys are used with. For compatibility with existing BIP 44 implementations, we use the same constants as defined in SLIP 44 6. Note that in keeping with that document, all cryptocurrency testnets share \(coin\_type\) index \(1\!\) .
• \(account\!\) : numbered from index \(0\) in sequentially increasing manner. Defined as in BIP 44 5.

Unlike BIP 44, none of the shielded key paths have a \(change\) path level. The use of change addresses in Bitcoin is a (failed) attempt to increase the difficulty of tracking users on the transaction graph, by segregating external and internal address usage. Shielded addresses are never publicly visible in transactions, which means that sending change back to the originating address is indistinguishable from using a change address.

Sapling key path

Sapling provides a mechanism to allow the efficient creation of diversified payment addresses with the same spending authority. A group of such addresses shares the same full viewing key and incoming viewing key, and so creating as many unlinkable addresses as needed does not increase the cost of scanning the block chain for relevant transactions.

The above key path levels include an account identifier, which in all user interfaces is represented as a "bucket of funds" under the control of a single spending authority. Therefore, wallets implementing Sapling ZIP 32 derivation MUST support the following path for any account in range \(\{ 0\,..\, 2^{31} - 1 \}\!\) :

• \(m_\mathsf{Sapling} / purpose' / coin\_type' / account'\!\) .

Furthermore, wallets MUST support generating the default payment address (corresponding to the default diversifier as defined above) for any account they support. They MAY also support generating a stream of payment addresses for a given account, if they wish to maintain the user experience of giving a unique address to each recipient.

Note that a given account can have a maximum of approximately \(2^{87}\) payment addresses, because each diversifier has around a 50% chance of being invalid.

If in certain circumstances a wallet needs to derive independent spend authorities within a single account, they MAY additionally support a non-hardened \(address\_index\) path level as in 5:

• \(m_\mathsf{Sapling} / purpose' / coin\_type' / account' / address\_index\!\) .

zcashd version 4.6.0 and later uses this to derive "legacy" Sapling addresses from a mnemonic seed phrase under account \(\mathtt{0x7FFFFFFF}\!\) , using hardened derivation for \(address\_index\!\) .

Orchard key path

Orchard supports diversified addresses with the same spending authority (like Sapling). A group of such addresses shares the same full viewing key and incoming viewing key, and so creating as many unlinkable addresses as needed does not increase the cost of scanning the block chain for relevant transactions.

The above key path levels include an account identifier, which in all user interfaces is represented as a "bucket of funds" under the control of a single spending authority. Therefore, wallets implementing Orchard ZIP 32 derivation MUST support the following path for any account in range \(\{ 0\,..\, 2^{31} - 1 \}\!\) :

• \(m_\mathsf{Orchard} / purpose' / coin\_type' / account'\!\) .

Furthermore, wallets MUST support generating the default payment address (corresponding to the default diversifier for Orchard) for any account they support. They MAY also support generating a stream of diversified payment addresses for a given account, if they wish to enable users to give a unique address to each recipient.

Note that a given account can have a maximum of \(2^{88}\) payment addresses (unlike Sapling, all Orchard diversifiers are valid).

Sapling Full Viewing Key Fingerprints and Tags

A "Sapling full viewing key fingerprint" of a full viewing key with raw encoding \(\mathit{FVK}\) (as specified in 18) is given by:

• \(\mathsf{BLAKE2b}\text{-}\mathsf{256}(\texttt{“ZcashSaplingFVFP”}, \mathit{FVK})\!\) .

It MAY be used to uniquely identify a particular Sapling full viewing key.

A "Sapling full viewing key tag" is the first 4 bytes of the corresponding Sapling full viewing key fingerprint. It is intended for optimizing performance of key lookups, and MUST NOT be assumed to uniquely identify a particular key.

Orchard Full Viewing Key Fingerprints and Tags

An "Orchard full viewing key fingerprint" of a full viewing key with raw encoding \(\mathit{FVK}\) (as specified in 20) is given by:

• \(\mathsf{BLAKE2b}\text{-}\mathsf{256}(\texttt{“ZcashOrchardFVFP”}, \mathit{FVK})\!\) .

It MAY be used to uniquely identify a particular Orchard full viewing key.

An "Orchard full viewing key tag" is the first 4 bytes of the corresponding Orchard full viewing key fingerprint. It is intended for optimizing performance of key lookups, and MUST NOT be assumed to uniquely identify a particular key.

Seed Fingerprints

A "seed fingerprint" for the master seed \(S\) of a hierarchical deterministic wallet is given by:

• \(\mathsf{BLAKE2b}\text{-}\mathsf{256}(\texttt{“Zcash\_HD\_Seed\_FP”},\) \([\mathsf{length}(S)]\,||\,S)\!\) .

It MAY be used to uniquely identify a particular hierarchical deterministic wallet.

No corresponding short tag is defined.

Note: a previous version of this specification did not have the length byte prefixing the seed. The current specification reflects the implementation in zcashd.

Sapling extended spending keys

A Sapling extended spending key \((\mathsf{ask, nsk, ovk, dk, c})\!\) , at depth \(depth\!\) , with parent full viewing key tag \(parent\_fvk\_tag\) and child number \(i\!\) , is represented as a byte sequence:

• \(\mathsf{I2LEOSP}_{8}(depth)\) \(||\,parent\_fvk\_tag\) \(||\,\mathsf{I2LEOSP}_{32}(i)\) \(||\,\mathsf{c}\) \(||\,\mathsf{EncodeExtSKParts}(\mathsf{ask, nsk, ovk, dk})\!\) .

For the master extended spending key, \(depth\) is \(0\!\) , \(parent\_fvk\_tag\) is 4 zero bytes, and \(i\) is \(0\!\) .

When encoded as Bech32, the Human-Readable Part is secret-extended-key-main for the production network, or secret-extended-key-test for the test network.

Sapling extended full viewing keys

A Sapling extended full viewing key \((\mathsf{ak, nk, ovk, dk, c})\!\) , at depth \(depth\!\) , with parent full viewing key tag \(parent\_fvk\_tag\) and child number \(i\!\) , is represented as a byte sequence:

• \(\mathsf{I2LEOSP}_{8}(depth)\) \(||\,parent\_fvk\_tag\) \(||\,\mathsf{I2LEOSP}_{32}(i)\) \(||\,\mathsf{c}\) \(||\,\mathsf{EncodeExtFVKParts}(\mathsf{ak, nk, ovk, dk})\!\) .

For the master extended full viewing key, \(depth\) is \(0\!\) , \(parent\_fvk\_tag\) is 4 zero bytes, and \(i\) is \(0\!\) .

When encoded as Bech32, the Human-Readable Part is zxviews for the production network, or zxviewtestsapling for the test network.

Orchard extended spending keys

An Orchard extended spending key \((\mathsf{sk, c})\!\) , at depth \(depth\!\) , with parent full viewing key tag \(parent\_fvk\_tag\) and child number \(i\!\) , is represented as a byte sequence:

• \(\mathsf{I2LEOSP}_{8}(depth)\,||\,parent\_fvk\_tag\,||\,\mathsf{I2LEOSP}_{32}(i)\,||\,\mathsf{c}\,||\,\mathsf{sk}\!\) .

For the master extended spending key, \(depth\) is \(0\!\) , \(parent\_fvk\_tag\) is 4 zero bytes, and \(i\) is \(0\!\) .

When encoded as Bech32, the Human-Readable Part is secret-orchard-extsk-main for Mainnet, or secret-orchard-extsk-test for Testnet.

We define this encoding for completeness, however given that it includes the capability to derive child spending keys, we expect that most wallets will only expose the regular Orchard spending key encoding to users 21.